Transport of Two-dimensional Electron Gas in Random Magnetic Field

<Japanese>

Why is it interesting?
Experimental Setup
Results

Why is it interesting?

The issue of two-dimensional electron system (2DES) in random magnetic field is of particular interest from some aspects.

(1) Anderson localization

It is well established that all electron states in the presence of potential randomness are localized. But the case of random magnetic field still remains controversial and there are some suggestions that extended state might exist in this case.

(2) Relevance to the composite fermion

Half-filled Landau level (HFLL), or $nu$=1/2 state of the quantum Hall system can be mapped to the zero-field state of a fictious particle called "composite fermion", a composite of one electron and two magnetic flux tubes. With this mapping, the random potential ( small, but unavoidable! ) is mapped to an effective magnetic field felt by the composite fermions. The characteristic feature in the magnetoresistance around the HFLL states (right figure) may have something to do with this random field.

The purpose of this to study the transport properties of a 2DES in a controlled random magnetic field and to give some clue to the above problems.

Magnetoresistance of a 2DEG around $nu$=1/2
Jiang et al. (1989)

Experimental Setup@

The sample is a Hallbar of GaAs 2DES decorated with randomly patterned magnetic film, an alloy of Dy and Cu. This material has a large saturation magnetic moment that makes a large field modulation on the 2DES, but does not have a spontaneous magnetization at helium temperature. So the amplitude of the field modulation can be controlled continuously from zero.

The actual sample looks like the right figure. The characteristic length scale of the randomness is about 1 micron. This is fairly shorter than the mean free path of the electron, which is about 10 micron.

Random field is produced by magnetizing the patterned DyCu by an external magnetic field. By applying this external field pararell to the 2D plane, a random field with practically zero mean is produced.

We also have a small magnet that can apply a uniform perpendicular field independently to the sample.

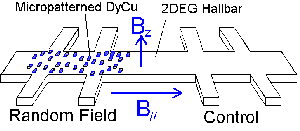
Schematic illustration of the sample

SEM image of the sample

Results

First to study the effect of zero-mean random field, a in-plane field is applied. It is obvious that the resistance of the random field sample (red line) shows a larger increase with increasing in-plane field than that of the control sample (blue line).

This increase in the resistivity is roughly proportional to the square of the magnetization of the DyCu film ( green marks: measured with SQUID magnetometer ).

Next, keeping the random field modulation fixed, we measured the magnetoresistance to uniform field component. The resistivity curve resembles that of a plain 2DES without random magnets, but in high field region around the HFLL state! The common features are

  • wide positive magnetoresistance and a downward cusp at origin
  • small temperature dependence of "low-field" part of the curve
  • the characteristic cusp structure at the origin is visible only when the mobility is fairly high

This implies the relevance between the composite fermion and random field problem.

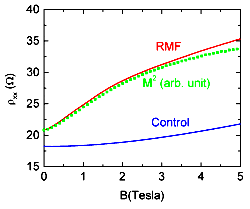
Dependence on in-plane field

Magnetoresistance in fixed random field component

Masato Ando <andom@issp.u-tokyo.ac.jp>