２次元系においてはポテンシャルのランダムネスのもとでは「すべての電子状態は局在する」とされています。しかし磁場がランダムな場合については現在でも多数の理論研究がなされており，非局在状態の存在する可能性などが指摘されています。

(2) 複合フェルミオンとの関連から

Half-filled Landau level, つまり量子ホール系で ν=1/2 にあたる状態との関連です。ν=1/2 状態というのは複合フェルミオンという電子に磁束２本を貼り付けた仮想粒子のゼロ磁場状態にマッピングされますが， このマッピングの際に，系にわずかですが必ず存在するランダムポテンシャルは，複合フェルミオンにとってのランダム磁場にマップされます。 つまり，ν=1/2 周辺で見られるこのような磁気抵抗の振る舞い（右図）がランダム磁場と関連があるかもしれないということです。

本研究は制御されたランダム磁場下での２次元電子系の伝導を調べること，またそれによってこれらの問題への手がかりを得ることを目的としています。

ν=1/2周辺の磁気抵抗
Jiang et al. (1989)

磁性体としてDyとCuの合金を用いたことがひとつの特徴です。 この物質はDyを含んでいるため体積あたりの飽和磁化が大きく，大きな変調磁場を作り出すことができる一方， 比較的低温でも自発磁化を持たないため，外部磁場によってその変調磁場の大きさをゼロから連続的にコントロールできるのが特徴です。

今回の試料では右図のようなパターンになっており，ランダム磁場を特徴付ける相関長が約１ミクロンで，電子の平均自由行程１０ミクロンよりも十分短くなっています。

ランダム磁場はこれらの磁性体を外部磁場によって磁化させることによって発生させるわけですが，２次元系に殆ど影響を及ぼさない面内方向の磁場で磁性体を磁化することによりゼロ平均の変調磁場を作り出せます。

また，それと直交するマグネットで２次元面に垂直な一様磁場をそれとは独立にかけることができます。

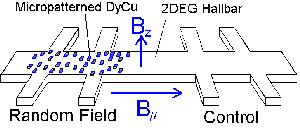
試料の概念図

試料のSEM写真

この抵抗の増加をランダム磁場の強さと比較したいわけですが， ここで磁性体がヒステリシスを持たないことが重要になってきます。 緑色の点は同時に蒸着したDyCuの磁化をSQUIDで測定したデータを２乗して適当にリスケールしたものですが，ランダム磁場による抵抗増加とほぼ一致することがわかります。

つぎに，面内方向の強い磁場をそのままにしてランダム変調を一定に保ちながら一様磁場成分を加えたときの磁気抵抗です。この磁気抵抗の形は上で紹介したν=1/2のまわりでの磁気抵抗（磁性体の修飾とかはない２次元電子系）とよく似た形をしています。これらの間の共通点としては

• 正の磁気抵抗とそれに付随して原点付近に見られる下向きのカスプ
• 高磁場領域の量子振動の大きな温度依存性に対して，低磁場側の構造は温度依存をあまりもたない
• 原点付近の特徴的な構造はどちらもモビリティが比較的大きい，つまり平均自由行程が十分に長い場合にのみ見られる。

などが挙げられます。これは複合フェルミオンとランダム磁場系の関連を示唆しています。

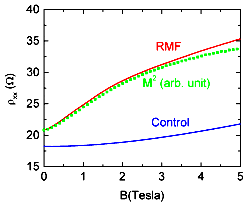
面内磁場に対する依存性

一定のランダム磁場下での磁気抵抗