1.はじめに
GaAs/AlGaAs半導体ヘテロ界面2次元電子系試料に微細加工をもつゲート電極を付加すると様々な形状のポテンシャル変調を人工的に作り出すことができる。本研究では空間変調磁場中での2次元電子系のふるまいについて研究している。磁場変調の振幅はワイス振動と呼ばれる磁気抵抗振動の解析から定量的に得ることができ、磁性金属ゲートの磁性体の種類や平行磁場の方位角によって制御できる。この系を用いて電子ー電子散乱による電気抵抗のを定量的に評価する実験を行っている。
2.試料
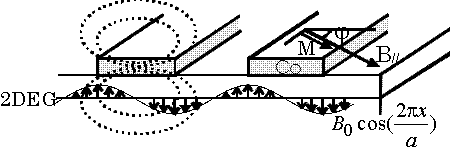
図1
試料は図1の様にGaAs/AlGaAsヘテロ接合の試料表面にすだれ状の強磁性体電極をつけたものである。2次元電子系にかけた磁場は同時に強磁性体を磁化させる役割を担っている。
2次元電子系に平行に十分強い磁場をかけることによって、2次元電子の軌道運動に影響を与えることなく強磁性体の磁化を飽和させることが可能である。又、平行磁場を面内で回転させることによって、磁性体の磁化方向をコントロールすることが可能である
3.磁気抵抗振動(磁気ワイス振動)

図2
図2は平行磁場を印加する角度を変えて系に垂直方向の磁場に対する磁気抵抗を測定した結果である。0.3T以下で見られる磁気抵抗振動が磁気ワイス振動である。
これは、周期的ポテンシャルの周期aと2次元電子のサイクロトロン直径2Rcの整合性に起因する現象で、2Rc/a=n+1/4(n=1,2,3...)の条件の時に磁気抵抗は極小となる。
磁気抵抗振動の振幅は磁場変調の振幅の二乗に比例するが、図2において平行磁場を印加する角度が大きくなるにつれ振幅が小さくなっている様子が観測された。

図3
図3は図2で得られた磁気抵抗振動の解析から磁場変調を求めた結果である。磁性体としてCoとNiを用いた。B0〜cos(φ)という予想通りの振る舞いが見られた。φ=90oつまり強磁性体長手方向に平行磁場をかけた場合は磁場変調はゼロとなる。
4.電子−電子散乱効果
このように定量的なコントロールが可能となった空間磁場変調を利用して、われわれは二次元電子系の電子電子散乱の効果について研究している。
電子−電子散乱による電気抵抗のT2-項は、重い電子系や有機伝導体など強相関系と呼ばれる物質をはじめとして様々な系で議論されている。
よく知られているように、自由電子モデルのような並進対称性を有する系では衝突する2電子の全運動量が保存するため電子−電子散乱は電気抵抗には寄与しない。
本研究の系は、
-
フォノン散乱などの他の散乱過程が良く分かっている。
-
周期ポテンシャルを導入することで並進対称性が破られる。
-
変調の大きさが分かっている。
-
電子密度を変えずに変調の大きさを変化させることができる。
という、電子−電子散乱の効果を定量的に調べるのに好適な系であると言える。
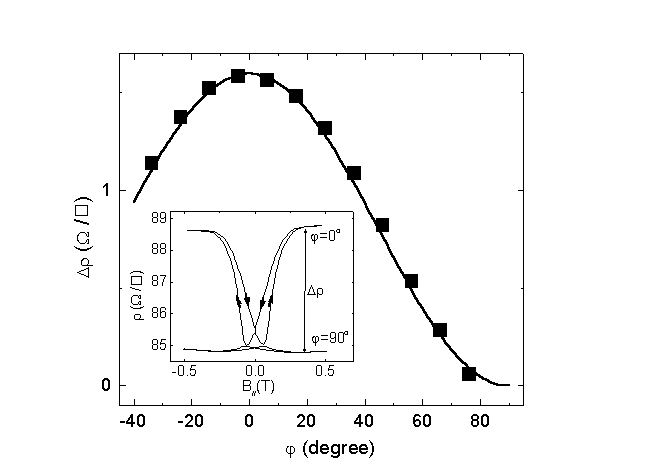
図4
図4の挿入図は垂直磁場ゼロの条件で、平行磁場に対する抵抗の変化を表したもので、方位角φ=0oとφ=90o(変調ゼロ)について示してある。平行磁場の役割は二次元電子の軌道運動に影響を与えず、すだれ状の強磁性体を磁化させることで、周期的磁場変調を作り出すものである。0.3Tの磁場で磁化も飽和しており、それを受けて抵抗も一定の値となっている。ここで、図中に示したΔρは磁場変調の印加により生じた散乱による抵抗の増加分である。
主図はΔρが平行磁場の方位角φに対してΔρ〜cos2φに従って変化していることを示している。先にみたように変調の振幅はB0〜cosφなので、Δρ〜B02となる。この事は、散乱確率が変調振幅の2乗となることより理解できる。
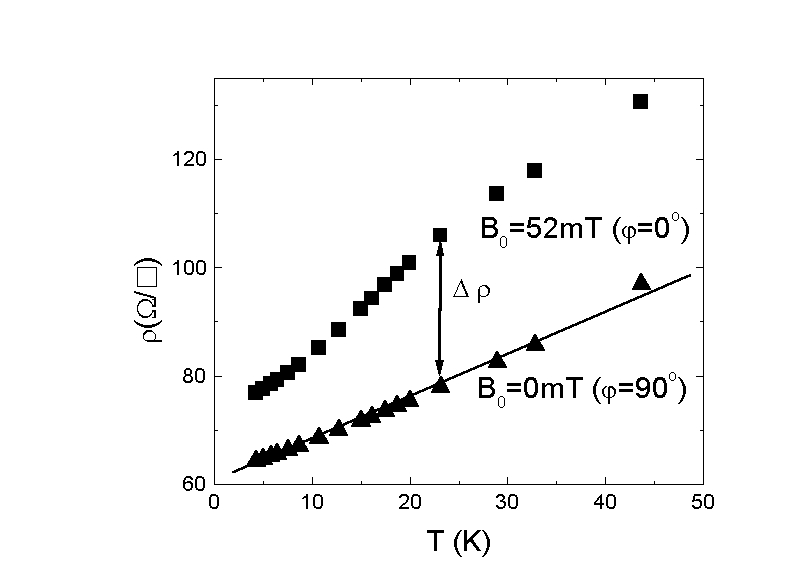
図5
図5は方位角φ=0oとφ=90o(変調ゼロ)について抵抗の温度変化を示してある。変調ゼロの場合は通常の音響フォノン散乱によるT-linearの温度依存性が観測されている。2つのデータの差がΔρに対応している。
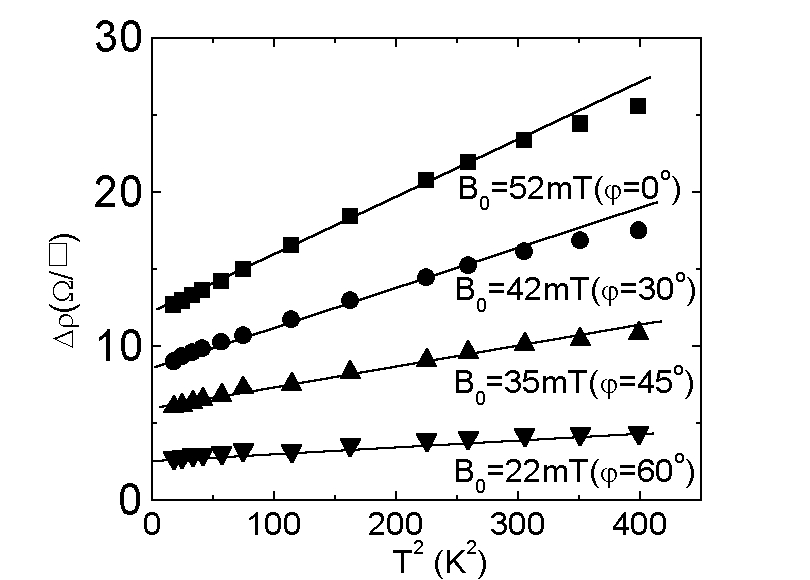
図6
図6は、いくつかのφの値に対して(いくつかの磁場変調の値)図5の実験から得られたΔρをT2に対してプロットしたものである。電子−電子散乱特有のT2の温度依存性が観測されている。
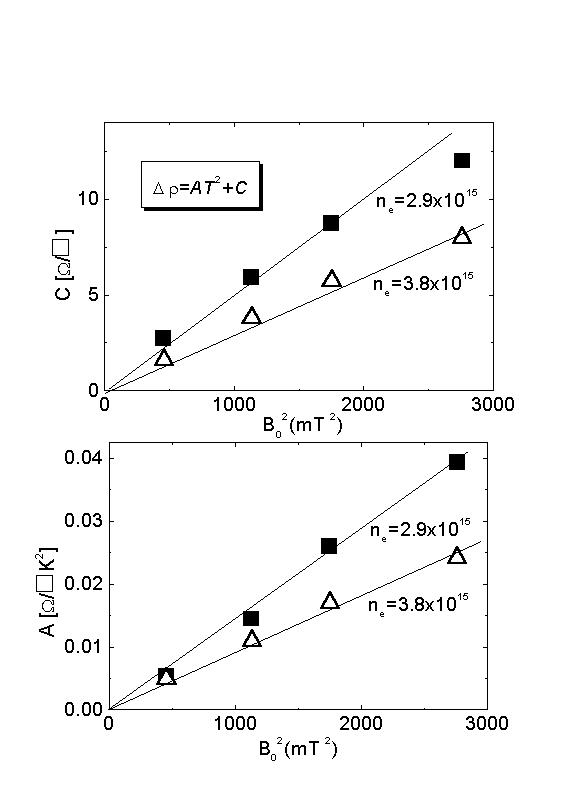
図7
図7は、電子密度の異なる2つの試料について図6で得られたΔρをAT2+Cと表し、それぞれB02に対してA、Cをプロットしたものである。AのB02の依存性は電子−電子散乱の強さに対応している事から理解できるが、Cについてはどうだろうか?
Δρは磁場変調により生じた散乱により抵抗が増加した分である。電子−電子散乱のT2
-項は、単純には、散乱の始状態と終状態の準位の熱的なKBTのボケによるものなので、絶対零度ではこの値は0になることが期待される。しかし、実験では有限の、しかもB02の依存性が得られた。これはいったい何故なのだろう?
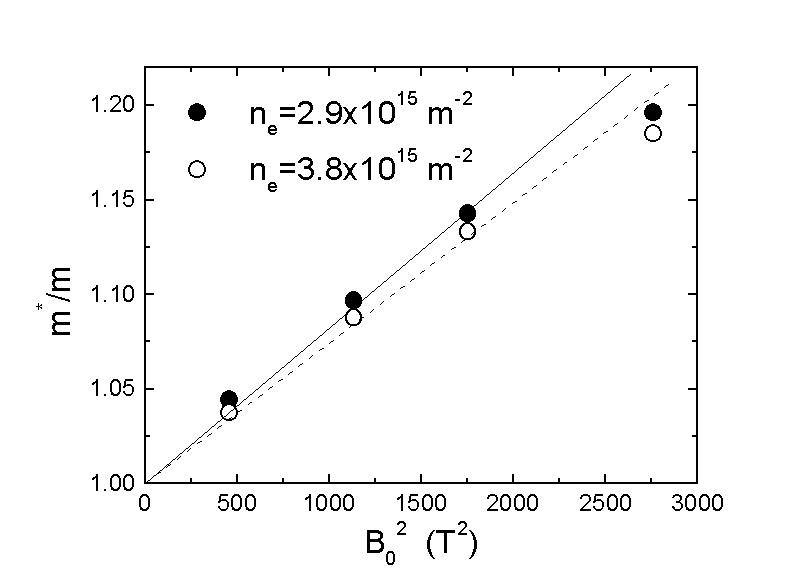
図8
先の理由を得るためには、電子の有効質量について考える必要がある。空間的磁場変調下では、系のエネルギー分散関係は、明らかに磁場変調の無い場合とは異なる。このエネルギーバンドの変化は電子の有効質量にも変化を与える。
ここで、磁場変調の無い場合の自由電子の質量をm、磁場変調のある場合の自由電子の質量をm*とすると、Drudeの公式により抵抗率は
1.磁場変調の無い場合 ρ0(T)=m/ne2τ(T)
1/τ(T)=1/τ0+α・T
2.磁場変調のある場合 ρ(T)=m*/ne2(1/τ(T)+1/τe-e(T))
1/τe-e(T)=A・T2
となる。 よって、絶対零度での抵抗率の変化Δρは、
Δρ(0)=ρ(0)-ρ0(0)=ρ0(0)・(m*/m-1)
と表され有限な値が期待される。 図8はこの式を用いてデータから見積もった有効質量の比を磁場変調の値の2乗に対してプロットしたものである。
|